题目来源于武老师的每日一题,答案是自己做的,不太严谨,仅供参考
2022年11月1日
知识点:函数定义域
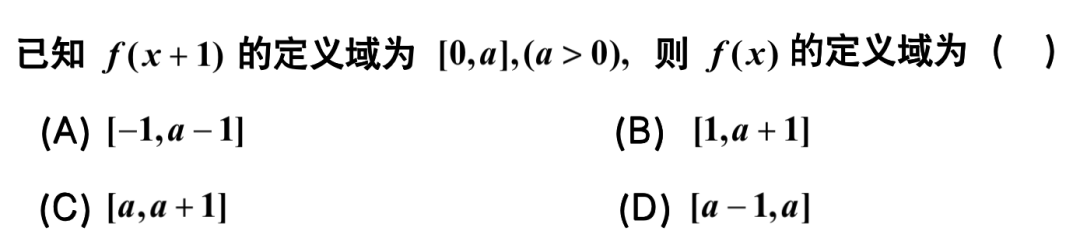
答案:
$$
\text{函数定义域是指自变量}x\text{的取值范围,不可以把}x+1\text{作为自变量,}x\text{才是自变量,}
\
\text{同一个}f()\text{,括号内整体范围相同。由题意得}0\leqslant x\leqslant a\Rightarrow 1\leqslant x+1\leqslant a+1\text{,所以}f\left( x \right) \text{定义域为}\left[ 1,a+1 \right]
$$
2022年11月2日
知识点:函数定义域
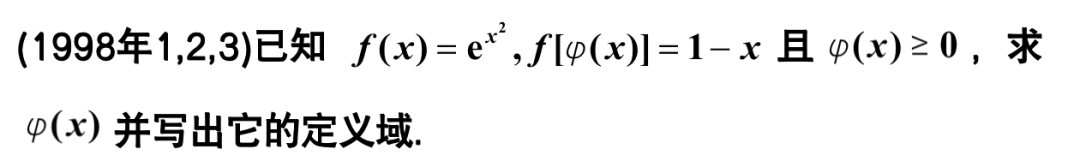
答案:
$$
f\left[ \varphi \left( x \right) \right] =1-x^2,f\left( x \right) ={e^x}^{^2}\Longrightarrow e^{\varphi ^2\left( x \right)}=1-x,\text{两边同时求}\ln ,\varphi ^2\left( x \right) =\ln \left( 1-x \right)
\
\text{由题意得}\varphi \left( x \right) \ge 0,\text{两边开根号},\varphi \left( x \right) =\sqrt{\ln \left( 1-x \right)},\text{负半边不要了,只留正的。定义域:}\ln \left( 1-x \right) \ge 0\Rightarrow 1-x\ge 1\Rightarrow x\le 0
$$
2022年11月3日
知识点:复合函数
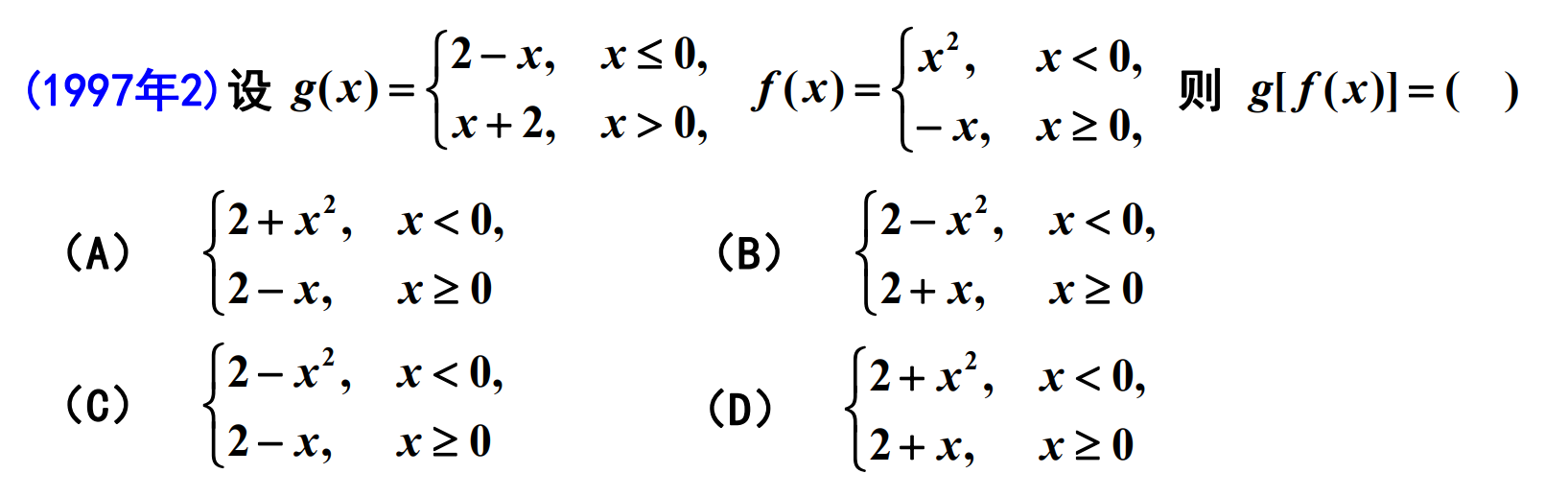
答案:
$$
g\left( x \right) =\begin{cases}
2-x, x\le 0\
x+2,x\ge 0\
\end{cases},f\left( x \right) =\begin{cases}
x^2, x<0\
-x,x\ge 0\
\end{cases},f\left( x \right) \text{是}g\left( x \right) \text{的复合函数}
\
x^2,x<0\text{但是}x^2>0,-x,x\ge 0\text{但是}-x<0,\text{所以}g\left[ f\left( x \right) \right] =\begin{cases}
2+x^{}, x\ge 0\
x^2+2,x<0\
\end{cases},\text{注意}x\text{的取值,与}f\left( x \right) \text{的取值是一致的}
$$
2022年11月4日
知识点:反函数
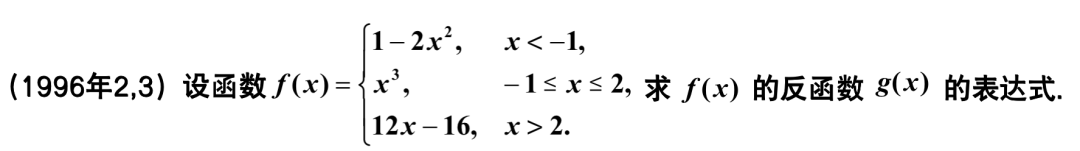
答案:
$$
\text{把}f\left( x \right) \text{分段拆开来看},\text{当}x<-1,y=1-2x^2\Rightarrow x=\pm \sqrt{\frac{1-y}{2}},\text{因为}x<-1,x=-\sqrt{\frac{1-y}{2}},x=-1\text{时},y=-1,\text{所以}x=-\sqrt{\frac{1-y}{2}},y<-1\text{。}
\
\text{当}-1\le x\le 2\text{时},y=x^3\Rightarrow x=\sqrt[3]{y},\text{当}x=-1\text{时},y=-1,\text{当}x=2\text{时},y=8\text{所以}x=\sqrt[3]{y},-1\le y\le 8\text{。}
\
\text{当}x>2\text{时},y=12x-16\Rightarrow x=\frac{y+16}{12},x=2,y=8,\text{所以}x=\frac{y+16}{12},y>8\text{。}
\
\text{把}y\text{换成}x,g\left( x \right) =\left{ \begin{array}{c}
-\sqrt{\frac{1-x}{2}},x<-1\
\sqrt[3]{x},-1\le x\le 8\
\frac{x+16}{12},x>8\
\end{array} \right.
$$
2022年11月5日
知识点:函数奇偶性
重点

答案:
$$
\text{设}h\left( x \right) \text{为奇函数,}g\left( x \right) \text{为偶函数可以使}f\left( x \right) =h\left( x \right) +g\left( x \right) \text{成立,}h\left( -x \right) =-h\left( x \right) ,g\left( -x \right) =g\left( x \right)
\
f\left( -x \right) =h\left( -x \right) +g\left( -x \right) =-h\left( x \right) +g\left( x \right) ,\left{ \begin{array}{c}
f\left( x \right) =h\left( x \right) +g\left( x \right)\
f\left( -x \right) =-h\left( x \right) +g\left( x \right)\
\end{array}\Rightarrow g\left( x \right) =\frac{1}{2}\left[ f\left( x \right) +f\left( -x \right) \right] \left( x\text{与}-x\text{互换等式结果一样,偶函数} \right) ,h\left( x \right) =\frac{1}{2}\left[ f\left( x \right) -f\left( -x \right) \right] \left( x\text{与}-x\text{互换等式结果一样,奇函数} \right) \right.
$$
2022年11月6日
知识点:函数基本性质
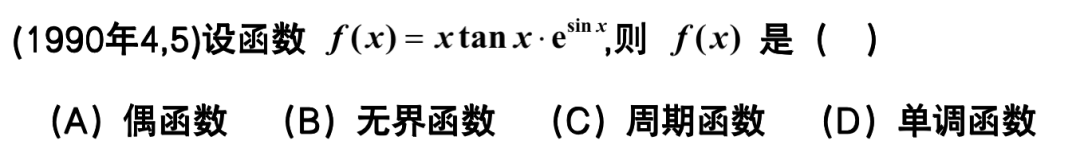
答案:
$$
f\left( -x \right) =-x\tan \left( -x \right) \cdot e^{\sin -x}=x\tan x\cdot e^{-\sin x},f\left( x \right) \ne f\left( x \right) ,A\text{错}
\
e^{\sin x}\text{为周期函数,}\tan x\text{为周期函数,}x\text{单调递增,相乘后不是周期函数,}C\text{错}
\
x,\tan x\text{在}\left( -\frac{\pi}{2},\frac{\pi}{2} \right) \text{上单调递增,}e^{\sin x}\text{为周期函数,则}f\left( x \right) \text{不是单调函数,}D\text{错,证明出}B\text{正确}
$$
2022年11月7日
知识点:函数的有界性
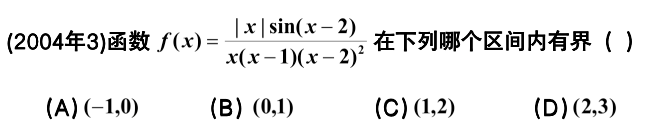
答案:
$$
\lim_{x\rightarrow -1} f\left( x \right) =\frac{-\sin 3}{-1\cdot -2\cdot 9}=\frac{\sin 3}{18},\lim_{x\rightarrow 0^-} f\left( x \right) =\frac{\sin 2}{-4},A\text{正确}
\
\lim_{x\rightarrow 0^+} f\left( x \right) =\frac{\sin 2}{4},\lim_{x\rightarrow 1^-} f\left( x \right) =\frac{1}{x-1}\cdot -\sin 1=-\infty ,B\text{错}
\
\lim_{x\rightarrow 1^+} f\left( x \right) =\frac{1}{x-1}\cdot -\sin 1=+\infty ,\lim_{x\rightarrow 2^-} f\left( x \right) =\frac{1}{x-2}=-\infty ,C\text{错}
\
\lim_{x\rightarrow 2^+} f\left( x \right) =\frac{1}{x-2}=+\infty \text{,}\lim_{x\rightarrow 3} f\left( x \right) =\frac{\sin 1}{2},D\text{错}
$$
2022年11月8日
知识点:极限的计算
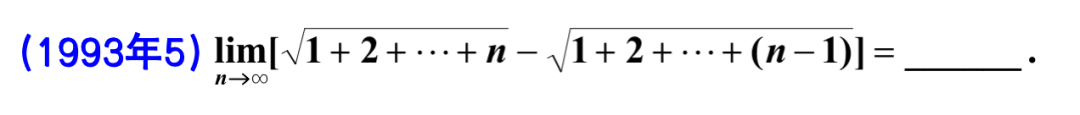
$$
\begin{aligned}
\text{原式}& =\lim_{n\rightarrow \infty} \left[ \sqrt{1+2+…+n}-\sqrt{1+2+…+\left( n-1 \right)} \right]
\
& =\lim_{n\rightarrow \infty} \left[ \sqrt{\frac{n\left( 1+n \right)}{2}}-\sqrt{\frac{\left( 1+n-1 \right) n}{2}} \right]
\
& =\lim_{n\rightarrow \infty} \left[ \sqrt{\frac{n\left( 1+n \right)}{2}}-\sqrt{\frac{n^2}{2}} \right]
\
& =\lim_{n\rightarrow \infty} \left[ \frac{\frac{n+n^2-n^2}{2}}{\sqrt{\frac{n\left( 1+n \right)}{2}}+\sqrt{\frac{n^2}{2}}} \right]
\
& =\sqrt{2}\lim_{n\rightarrow \infty} \left[ \frac{1}{\sqrt{1+\frac{1}{n}}+\sqrt{1}} \right]
\
& =\frac{\sqrt{2}}{2}
\end{aligned}
$$
2022年11月9日
知识点:极限的计算
注意根号下x的平方,在x<0时,得到的值是负值
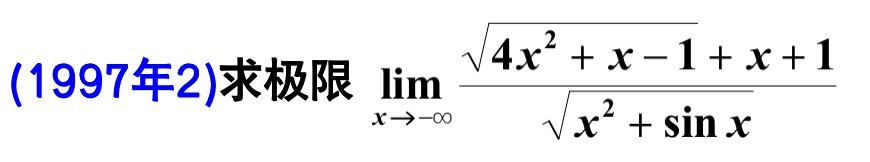
答案:
法一(直接法):
$$
\begin{aligned}
\text{原式}& =\lim_{x\rightarrow -\infty} \frac{\left( -x \right) \left[ \sqrt{4+\frac{1}{x}-\frac{1}{x^2}}-1-\frac{1}{x} \right]}{\left( -x \right) \sqrt{1+\frac{\sin x}{x^2}}}
\
& =\lim_{x\rightarrow -\infty} \frac{\sqrt{4+\frac{1}{x}-\frac{1}{x^2}}-1-\frac{1}{x}}{\sqrt{1+\frac{\sin x}{x^2}}}\left( x<0,\sqrt{x^2}<0 \right)
\
& =1
\end{aligned}
$$
法二(抓大头):
$$
\begin{aligned}
\text{原式}& =\lim_{x\rightarrow -\infty} \frac{\sqrt{4x^2}+x}{\sqrt{x^2}}
\
& =\lim_{x\rightarrow -\infty} \frac{-2x+x}{-x}
\
& =1
\end{aligned}
$$
2022年11月10日
知识点:判别左右极限

答案:
$$
\begin{aligned}
\text{原式}& =\lim_{x\rightarrow 0^+} \left( \frac{2+e^{\frac{1}{x}}}{1+e^{\frac{4}{x}}}+\frac{\sin x}{\left| x \right|} \right)
\
& =\lim_{x\rightarrow 0^+} \left( 0+1 \right) ,, \left( e^{\frac{4}{x}}\text{比}e^{\frac{1}{x}}\text{增长快} \right)
\
& =1
\
\text{原式}& =\lim_{x\rightarrow 0^-} \left( \frac{2+e^{\frac{1}{x}}}{1+e^{\frac{4}{x}}}+\frac{\sin x}{\left| x \right|} \right)
\
& =\lim_{x\rightarrow 0^-} \left( \frac{2+0}{1+0}+\frac{\sin x}{-x} \right)
\
& =\left( 2-1 \right)
\
& =1
\
\lim_{x\rightarrow 0^+} \text{左}&=\lim_{x\rightarrow 0^-} \text{右}=1
\end{aligned}
$$
2022年11月11日
知识点:四种方法计算极限
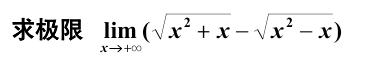
答案:
法一(直接法):
$$
\begin{aligned}
\text{法一:原式}&=\lim_{x\rightarrow \infty} \left( \frac{x^2+x-x^2+x}{\sqrt{x^2+x}+\sqrt{x^2-x}} \right)
\
&=\lim_{x\rightarrow \infty} \left( \frac{2x}{\sqrt{x^2+x}+\sqrt{x^2-x}} \right)
\
&=\lim_{x\rightarrow \infty} \left( \frac{2}{\sqrt{1+\frac{1}{x}}+\sqrt{1-\frac{1}{x}}} \right)
\
&=1
\end{aligned}
$$
法二(拉格朗日):
$$
\text{法二:设}f\left( x \right) =\sqrt{x}
\
\text{根据拉格朗日中值定理,}f\left( x^2+x \right) -f\left( x^2-x \right) =f\prime\left( \xi \right) \left( x^2+x-x^2+x \right) =2xf\prime\left( \xi \right) \text{,}\xi \text{介于}x^2+x\text{与}x^2-x\text{之间,}\xi \sim x^2,f\prime\left( \xi \right) =\frac{1}{2\sqrt{\xi}}
\
\text{原式}=\lim_{x\rightarrow \infty} 2xf\prime\left( \xi \right) =\lim_{x\rightarrow \infty} \frac{x}{\sqrt{\xi}}=1
$$
法三(常见等价无穷小):
$$
\begin{aligned}
\text{法三:原式}&=\lim_{x\rightarrow \infty} \sqrt{x^2-x}\left[ \sqrt{1+\frac{2x}{x^2-x}}-1 \right]
\
&=\lim_{x\rightarrow \infty} \sqrt{x^2-x}\cdot \frac{1}{x}\cdot \frac{2x}{x^2-x}
\
&=1
\end{aligned}
$$
法四(等价无穷小相减,减项不等价的话,可以用等价无穷小减):
$$
\begin{aligned}
\text{法四:原式}&=\lim_{x\rightarrow \infty} x\left( \sqrt{1+\frac{1}{x}}-\sqrt{1-\frac{1}{x}} \right)
\
&=\lim_{x\rightarrow \infty} x\left( \left( \sqrt{1+\frac{1}{x}}-1 \right) -\left( \sqrt{1-\frac{1}{x}}-1 \right) \right)
\
&=\lim_{x\rightarrow \infty} x\left( \frac{1}{2x}+\frac{1}{2x} \right)
\
&=1
\end{aligned}
$$
2022年11月12日
知识点:三种方法计算极限
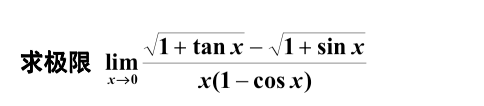
答案:
法一(直接法):
$$
\begin{aligned}
\text{法一:原式}&=\lim_{x\rightarrow 0} \frac{1+\tan x-1-\sin x}{x\left( 1-\cos \right) \left( \sqrt{1+\tan x}+\sqrt{1+\sin x} \right)}
\
&=\lim_{x\rightarrow 0} \frac{\tan x-\sin x}{\frac{1}{2}x^3\cdot 2}
\
&=\lim_{x\rightarrow 0} \frac{\tan x-\sin x}{x^3}
\
&=\lim_{x\rightarrow 0} \frac{x+\frac{x^3}{3}-\left( x-\frac{x^3}{6} \right) +o\left( x \right)}{x^3}
\
&=\frac{1}{2}
\end{aligned}
$$
法二(拉格朗日中值定理):
$$
\text{法二:设}f\left( x \right) =\sqrt{x}\text{,根据拉格朗日中值定理,}f\left( 1+\tan x \right) -f\left( 1+\sin x \right) =f\prime\left( \xi \right) \left( \tan x-\sin x \right)
\
\text{原式}=\lim_{x\rightarrow 0} \frac{f\prime\left( \xi \right) \left( \tan x-\sin x \right)}{\frac{1}{2}x^3}
\
\xi \text{在}1+\tan x\text{与}1+\sin x\text{之间,}x\text{趋于}0\text{,}1+\tan x\text{与}1+\sin x\text{都趋于}0\text{,根据夹逼定理,}\xi \sim 1
\
\begin{aligned}
\text{原式}&=\lim_{x\rightarrow 0} \frac{\frac{1}{2}\left( \tan x-\sin x \right)}{\frac{1}{2}x^3}
\
&=\lim_{x\rightarrow 0} \frac{\tan x-\sin x}{x^3}
\
&=\lim_{x\rightarrow 0} \frac{x+\frac{x^3}{3}-\left( x-\frac{x^3}{6} \right) +o\left( x \right)}{x^3}
\
&=\frac{1}{2}
\end{aligned}
$$
法三(等价无穷小):
$$
\begin{aligned}
\text{法三:原式}&=\lim_{x\rightarrow 0} \frac{\sqrt{1+\tan x}-\sqrt{1+\sin x}}{\frac{1}{2}x^3}
\
&=\lim_{x\rightarrow 0} \frac{\sqrt{\tan x+1}-1-\left( \sqrt{1+\sin x}-1 \right)}{\frac{1}{2}x^3}
\
&=\lim_{x\rightarrow 0} \frac{\frac{1}{2}\tan x-\frac{1}{2}\sin x}{\frac{1}{2}x^3}
\
&=\lim_{x\rightarrow 0} \frac{\tan x-\sin x}{x^3}
\
&=\lim_{x\rightarrow 0} \frac{x+\frac{x^3}{3}-\left( x-\frac{x^3}{6} \right) +o\left( x \right)}{x^3}
\
&=\frac{1}{2}
\end{aligned}
$$
2022年11月13日
知识点:求极限确定参数
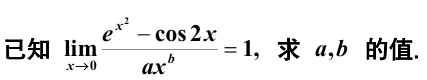
答案:
法一(直接法):
$$
\begin{aligned}
原式&=\lim_{x \to 0 } \frac{e^{x^{2}}-1-(cos2x-1) }{ax^{b}}
\
&=\lim_{x \to 0 } \frac{x^{2}+2x^{2} }{ax^{b}}
\
&= \lim_{x \to 0 } \frac{3x^{2} }{ax^{b}}=1
\
所以a&=3,b=2
\end{aligned}
$$
法二(泰勒公式):
$$
\begin{aligned}
原式&=\lim_{x \to 0 } \frac{(1+x^{2} )-(1-2x^{2} ) }{ax^{b}}
\
&=\lim_{x \to 0 } \frac{3x^{2} }{ax^{b}}=1
\
所以a&=3,b=2
\end{aligned}
$$
2022年11月14日
知识点:等价无穷小

答案:
$$
x\rightarrow 0,\varphi \left( x \right) =0,A\text{错,若要满足}ABCD\text{,}\varphi \left( x \right) \text{不能为}0
\
\text{可以认为极端情况}\varphi \left( x \right) \equiv 0\text{,都错,假如加上条件}\varphi \left( x \right) \ne 0\text{则都对}
\
\text{书上的条件是}\lim_{\varDelta \rightarrow 0} \frac{\sin \varDelta}{\varDelta}=1\text{,做这种题要注意}\varphi \left( x \right) \text{的取值}
$$
2022年11月15日
知识点:求极限
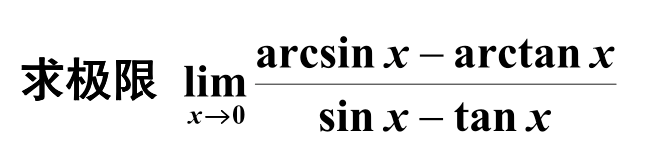
答案:
$$
\begin{aligned}
\text{原式}&=\lim_{x\rightarrow 0} \frac{x+\frac{x^3}{6}-\left( x-\frac{x^3}{3} \right)}{x-\frac{x^3}{6}-\left( x+\frac{x^3}{3} \right)}
\
&=\lim_{x\rightarrow 0} \frac{\frac{x^3}{2}}{-\frac{x^3}{2}}
\
&=-1
\end{aligned}
$$
2022年11月16日
知识点:求极限
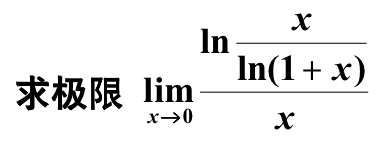
答案:
法一(直接法):
$$
\begin{aligned}
\text{原式}&=\lim_{x\rightarrow 0} \frac{\ln \frac{x}{\ln \left( 1+x \right)}+1-1}{x}
\
&=\lim_{x\rightarrow 0} \frac{\frac{x}{\ln \left( 1+x \right)}-1}{x}
\
&=\lim_{x\rightarrow 0} \frac{\frac{x-\ln \left( 1+x \right)}{\ln \left( 1+x \right)}}{x}
\
&=\lim_{x\rightarrow 0} \frac{x-\ln \left( 1+x \right)}{x\ln \left( 1+x \right)}
\
&=\lim_{x\rightarrow 0} \frac{x-\left( x-\frac{x^2}{2} \right)}{x^2}
\
&=\lim_{x\rightarrow 0} \frac{\frac{x^2}{2}}{x^2}
\
&=\frac{1}{2}
\end{aligned}
$$
法二(拉格朗日中值定理):
$$
\text{原式}=\lim_{x\rightarrow 0} \frac{\ln x-\ln \left( \ln \left( 1+x \right) \right)}{x},\text{设}f\left( x \right) =\ln x,\text{由拉格朗日中值定理得}f\left( x \right) -f\left( \ln \left( 1+x \right) \right) =f\prime\left( \xi \right) \left( x-\ln \left( 1+x \right) \right)
\
\frac{\xi}{x}\text{介于}\frac{x}{x}\text{与}\frac{\ln \left( x+1 \right)}{x}\text{之间,}x\text{趋于}0,\frac{x}{x}\rightarrow 1,\frac{\ln \left( 1+x \right)}{x}\rightarrow 1\text{,}\frac{\xi}{x}\rightarrow 1,\text{原式}=\lim_{x\rightarrow 0} \frac{f\prime\left( \xi \right) \left( x-\ln \left( 1+x \right) \right)}{x}=\lim_{x\rightarrow 0} \frac{\frac{x^2}{2}}{\xi x}=\frac{1}{2}\lim_{x\rightarrow 0} \frac{x}{\xi}=\frac{1}{x}
$$
2022年11月17日
知识点:小心经错标零

答案:
$$
\begin{aligned}
\text{原式}&=\lim_{x\rightarrow \infty} \frac{e^x}{ { e^x }^{^2\ln \left( 1+\frac{1}{x} \right) } }
\
&=\lim_{x\rightarrow \infty} e^{x-x^2\ln \left( 1+\frac{1}{x} \right)}
\
&=\lim_{x\rightarrow \infty} e^{x^2\left( \frac{1}{x}-\ln \left( 1+\frac{1}{x} \right) \right)}
\
&=e^{\frac{1}{2}}
\end{aligned}
$$
$$
\text{有二级结论}x-\ln \left( 1+x \right) \sim \frac{1}{2}x^2
$$
2022年11月18日
知识点:求极限
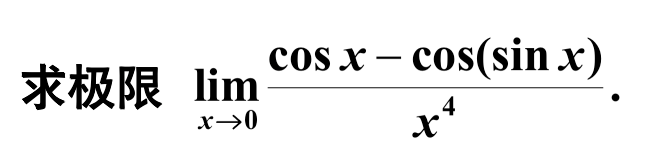
答案:
$$
\begin{aligned}
\text{设}f\left( x \right) &=\cos x,f\left( x \right) -f\left( \sin x \right) =f\prime\left( \xi \right) \left( x-\sin x \right) ,\xi \text{介于}x\text{与}\sin x\text{之间},\text{所以}\xi \rightarrow 0
\
\text{原式}&=\lim_{x\rightarrow 0} \frac{f\prime\left( \xi \right) \left( x-\sin x \right)}{x^4}
\
&=\lim_{x\rightarrow 0} \frac{-\sin \xi \left( x-\sin x \right)}{x^4}
\
&=-\lim_{x\rightarrow 0} \frac{x-\sin x}{x^3}
\
&=-\lim_{x\rightarrow 0} \frac{\frac{1}{6}x^3}{x^3}
\
&=-\frac{1}{6}
\end{aligned}
$$
2022年11月19日
知识点:求极限(偶数年真题)

$$
\begin{aligned}
设f(x)&=arctanx,f(x+1)-f(x)=f\prime (\xi )(x+1-x),f\prime (\xi )=\frac{1}{1+\xi^2} ,
\xi 介于x与x+1之间,x\rightarrow \infty ,\xi \rightarrow \infty
\
原式&=\lim_{x \to\infty }x^2[f\prime (\xi )]
\
&=\lim_{x \to\infty }\frac{x^2}{1+\xi ^2}
\
&=1
\end{aligned}
$$




