github库链接:https://github.com/stanford-cs336/spring2025-lectures
概述 本讲将讨论训练模型所需的所有基本要素,从张量到底层模型,再到优化器和训练循环。我们将密切关注效率(资源利用)。
资源类型
内存核算 张量基础 张量是存储所有内容(参数、梯度、优化器状态、数据、激活)的基本构建块。PyTorch 提供了强大的张量操作功能。
PyTorch 中创建张量的方法:
1 2 3 4 5 6 7 8 9 10 11 12 13 import torchx = torch.tensor([[1. , 2 , 3 ], [4 , 5 , 6 ]]) print (f"torch.tensor: {x} " )x = torch.zeros(4 , 8 ) print (f"torch.zeros (4x8):\n{x} " )x = torch.ones(4 , 8 ) print (f"torch.ones (4x8):\n{x} " )x = torch.randn(4 , 8 ) print (f"torch.randn (4x8):\n{x} " )
分配但不初始化值:
1 2 3 4 5 6 7 8 9 import torchfrom torch import nnx = torch.empty(4 , 8 ) print (f"torch.empty (4x8):\n{x} " )nn.init.trunc_normal_(x, mean=0 , std=1 , a=-2 , b=2 ) print (f"Initialized with trunc_normal_:\n{x} " )
张量内存 几乎所有内容都存储为浮点数。理解不同数据类型的内存占用对优化模型至关重要。
float32 (单精度)
默认数据类型,传统科学计算的基准。
内存使用量由值数量和数据类型决定。每个 float32 占用 4 字节。
1 2 3 4 5 6 7 8 9 10 11 12 import torchx = torch.zeros(4 , 8 ) print (f"Tensor dtype: {x.dtype} " )print (f"Number of elements: {x.numel()} " )print (f"Size of each element (bytes): {x.element_size()} " )print (f"Total memory usage (bytes): {x.numel() * x.element_size()} " )print (f"Memory for 12288*4 x 12288 matrix (float32): {12288 * 4 * 12288 * 4 / (1024 **3 ):.2 f} GB" )
float16 (半精度)
内存减半。每个 float16 占用 2 字节。
动态范围(特别是小数字)不佳,可能导致下溢,训练不稳定。
1 2 3 4 5 6 7 8 9 import torchx = torch.zeros(4 , 8 , dtype=torch.float16) print (f"Tensor dtype: {x.dtype} " )print (f"Size of each element (bytes): {x.element_size()} " )x_underflow = torch.tensor([1e-8 ], dtype=torch.float16) print (f"1e-8 in float16: {x_underflow} (可能为0,表示下溢)" )
bfloat16
Google Brain 于 2018 年开发,解决 float16 的下溢问题。
与 float16 内存相同,但指数位与 float32 相同,因此动态范围与 float32 相同。
分辨率较差,但对深度学习影响较小。
1 2 3 4 5 6 7 8 9 10 import torchx = torch.tensor([1e-8 ], dtype=torch.bfloat16) print (f"1e-8 in bfloat16: {x} (不会下溢)" )print ("\n--- Data Type Info ---" )print (f"float32: {torch.finfo(torch.float32)} " )print (f"float16: {torch.finfo(torch.float16)} " )print (f"bfloat16: {torch.finfo(torch.bfloat16)} " )
fp8
训练影响
使用 float32 训练可行,但需要大量内存。
使用 fp8、float16 和 bfloat16 训练有风险,可能导致不稳定。
解决方案:混合精度训练(稍后讨论)。
计算核算 GPU 上的张量 默认情况下,张量存储在 CPU 内存中。为了利用 GPU 的大规模并行性,需要将它们移动到 GPU 内存。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 import torchx = torch.zeros(32 , 32 ) print (f"Initial tensor device: {x.device} " )if torch.cuda.is_available(): print (f"Number of CUDA devices: {torch.cuda.device_count()} " ) for i in range (torch.cuda.device_count()): properties = torch.cuda.get_device_properties(i) print (f"Device {i} properties: {properties.name} " ) y = x.to("cuda:0" ) print (f"Tensor moved to GPU device: {y.device} " ) z = torch.zeros(32 , 32 , device="cuda:0" ) print (f"Tensor created directly on GPU device: {z.device} " ) else : print ("CUDA is not available. Cannot move tensors to GPU." )
张量操作 大多数张量是通过对其他张量执行操作而创建的。每个操作都有内存和计算后果。
张量存储 PyTorch 张量是指向已分配内存的指针,带有描述如何获取张量任何元素的元数据。这使得切片和视图操作非常高效。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 import torchx = torch.tensor([ [0. , 1 , 2 , 3 ], [4 , 5 , 6 , 7 ], [8 , 9 , 10 , 11 ], [12 , 13 , 14 , 15 ], ]) print (f"Tensor strides: {x.stride()} " )print (f"Stride for dimension 0 (rows): {x.stride(0 )} " )print (f"Stride for dimension 1 (columns): {x.stride(1 )} " )r, c = 1 , 2 index = r * x.stride(0 ) + c * x.stride(1 ) print (f"Calculated index for element ({r} ,{c} ): {index} " )print (f"Value at calculated index: {x.flatten()[index]} " )
张量切片 许多操作只是提供张量的不同“视图”,不进行复制。这意味着它们共享底层存储,因此一个张量的修改会影响另一个。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 import torchx = torch.tensor([[1. , 2 , 3 ], [4 , 5 , 6 ]]) print (f"Original tensor x:\n{x} " )y_row = x[0 ] print (f"View of row 0 (y_row): {y_row} " )y_col = x[:, 1 ] print (f"View of column 1 (y_col): {y_col} " )y_view = x.view(3 , 2 ) print (f"View as 3x2 (y_view):\n{y_view} " )y_transpose = x.transpose(1 , 0 ) print (f"Transposed view (y_transpose):\n{y_transpose} " )x[0 ][0 ] = 100 print (f"x after modification: {x} " )print (f"y_row after x modification: {y_row} " ) print (f"y_transpose after x modification: {y_transpose} " ) x_non_contiguous = torch.tensor([[1. , 2 , 3 ], [4 , 5 , 6 ]]) y_non_contiguous = x_non_contiguous.transpose(1 , 0 ) print (f"Is y_non_contiguous contiguous? {y_non_contiguous.is_contiguous()} " )y_contiguous = y_non_contiguous.contiguous().view(2 , 3 ) print (f"Is y_contiguous contiguous? {y_contiguous.is_contiguous()} " )print (f"y_contiguous after contiguous() and view:\n{y_contiguous} " )
逐元素操作 这些操作对张量的每个元素应用一些操作,并返回相同形状的新张量。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 import torchx = torch.tensor([1 , 4 , 9 ], dtype=torch.float32) print (f"Original tensor x: {x} " )print (f"x.pow(2): {x.pow (2 )} " ) print (f"x.sqrt(): {x.sqrt()} " ) print (f"x.rsqrt(): {x.rsqrt()} " ) print (f"x + x: {x + x} " ) print (f"x * 2: {x * 2 } " ) print (f"x / 0.5: {x / 0.5 } " ) x_triu = torch.ones(3 , 3 ) print (f"Original 3x3 tensor:\n{x_triu} " )print (f"x_triu.triu():\n{x_triu.triu()} " )
矩阵乘法 矩阵乘法是深度学习的核心操作,尤其是在神经网络层中。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 import torchx = torch.ones(16 , 32 ) w = torch.ones(32 , 2 ) y = x @ w print (f"Shape of x: {x.size()} " )print (f"Shape of w: {w.size()} " )print (f"Shape of y (x @ w): {y.size()} " )x_batch = torch.ones(4 , 8 , 16 , 32 ) w_weight = torch.ones(32 , 2 ) y_output = x_batch @ w_weight print (f"Shape of x_batch: {x_batch.size()} " )print (f"Shape of w_weight: {w_weight.size()} " )print (f"Shape of y_output (x_batch @ w_weight): {y_output.size()} " )
Einops Einops 是一个用于操作命名维度张量的库,灵感来自爱因斯坦求和约定。它提供了一种更直观、更不易出错的方式来重塑、转置和聚合张量。
Jaxtyping 基础 Jaxtyping 是一种类型提示工具,用于在代码中明确张量的维度名称,提高代码可读性和可维护性(仅作文档,不强制执行)。
1 2 3 4 5 6 7 8 9 10 11 import torchfrom jaxtyping import Floatx_old = torch.ones(2 , 2 , 1 , 3 ) print (f"Old way tensor shape: {x_old.shape} " )x_new: Float[torch.Tensor, "batch seq heads hidden" ] = torch.ones(2 , 2 , 1 , 3 ) print (f"New way (jaxtyping) tensor shape: {x_new.shape} " )
Einops Einsum einsum 是带有良好簿记的广义矩阵乘法。它允许通过指定输入和输出张量的维度名称来执行复杂的张量操作。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 import torchfrom einops import einsumfrom jaxtyping import Floatx: Float[torch.Tensor, "batch seq1 hidden" ] = torch.ones(2 , 3 , 4 ) y: Float[torch.Tensor, "batch seq2 hidden" ] = torch.ones(2 , 3 , 4 ) print (f"Shape of x: {x.shape} " )print (f"Shape of y: {y.shape} " )z_old = x @ y.transpose(-2 , -1 ) print (f"Old way (x @ y.transpose): {z_old.shape} " )z_new = einsum(x, y, "batch seq1 hidden, batch seq2 hidden -> batch seq1 seq2" ) print (f"New way (einops einsum): {z_new.shape} " )z_broadcast = einsum(x, y, "... seq1 hidden, ... seq2 hidden -> ... seq1 seq2" ) print (f"Einops einsum with broadcast (...): {z_broadcast.shape} " )
Einops Reduce reduce 允许通过一些操作(例如 sum, mean, max, min)减少单个张量。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 import torchfrom einops import reducefrom jaxtyping import Floatx: Float[torch.Tensor, "batch seq hidden" ] = torch.ones(2 , 3 , 4 ) print (f"Original tensor x shape: {x.shape} " )y_old = x.mean(dim=-1 ) print (f"Old way (x.mean(dim=-1)): {y_old.shape} " )y_new = reduce(x, "... hidden -> ..." , "sum" ) print (f"New way (einops reduce sum): {y_new.shape} " )y_mean = reduce(x, "... hidden -> ..." , "mean" ) print (f"New way (einops reduce mean): {y_mean.shape} " )
Einops Rearrange rearrange 用于重塑张量,当一个维度实际上代表两个或多个逻辑维度时,可以将其拆分或组合。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 import torchfrom einops import rearrange, einsumfrom jaxtyping import Floatx: Float[torch.Tensor, "batch seq total_hidden" ] = torch.ones(2 , 3 , 8 ) print (f"Original tensor x shape: {x.shape} " )x_rearranged = rearrange(x, "... (heads hidden1) -> ... heads hidden1" , heads=2 ) print (f"After rearrange (split total_hidden): {x_rearranged.shape} " )w: Float[torch.Tensor, "hidden1 hidden2" ] = torch.ones(4 , 4 ) print (f"Weight matrix w shape: {w.shape} " )x_transformed = einsum(x_rearranged, w, "... hidden1, hidden1 hidden2 -> ... hidden2" ) print (f"After einsum (transform hidden1 to hidden2): {x_transformed.shape} " )x_combined = rearrange(x_transformed, "... heads hidden2 -> ... (heads hidden2)" ) print (f"After rearrange (combine heads and hidden2): {x_combined.shape} " )
张量操作 FLOPs 浮点运算 (FLOP) 是基本操作,如加法或乘法。计算 FLOPs 对于评估模型计算成本至关重要。
线性层 FLOPs 对于一个输入 x (B, D),权重 w (D, K),输出 y (B, K) 的线性层 y = x @ w,其 FLOPs 计算如下:
矩阵乘法 x @ w:每个输出元素 y_ik 是 sum_j (x_ij * w_jk)。这涉及到 D 次乘法和 D-1 次加法。总共 2D-1 次浮点运算。对于 B * K 个输出元素,总 FLOPs 大约为 B * K * (2D - 1),近似为 2 * B * D * K。
1 2 3 4 B, D, K = 16 , 32 , 2 flops_linear_layer = 2 * B * D * K print (f"FLOPs for a linear layer (B={B} , D={D} , K={K} ): {flops_linear_layer} " )
激活函数 FLOPs
ReLU(x): 对于每个元素,进行一次比较和一次可能的赋值,通常算作 B * D FLOPs。Softmax(x): 涉及到指数运算和除法。对于 B * D 的张量,大约是 2 * B * D FLOPs。
损失函数 FLOPs
MSELoss(x, y) (均方误差损失): (x - y)^2 涉及一次减法、一次乘法(平方),然后求和求平均。大约 3 * B * D FLOPs。
梯度基础 PyTorch 使用自动微分(反向传播)计算梯度。loss.backward() 会计算所有 requires_grad=True 的张量的梯度,并存储在 param.grad 属性中。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 import torchx = torch.tensor([1.0 , 2.0 , 3.0 ], requires_grad=True ) w = torch.tensor([0.5 , 1.0 , 1.5 ], requires_grad=True ) y = x * w loss = y.sum () print (f"x: {x} " )print (f"w: {w} " )print (f"y: {y} " )print (f"loss: {loss} " )loss.backward() print (f"Gradient of x: {x.grad} " )print (f"Gradient of w: {w.grad} " )
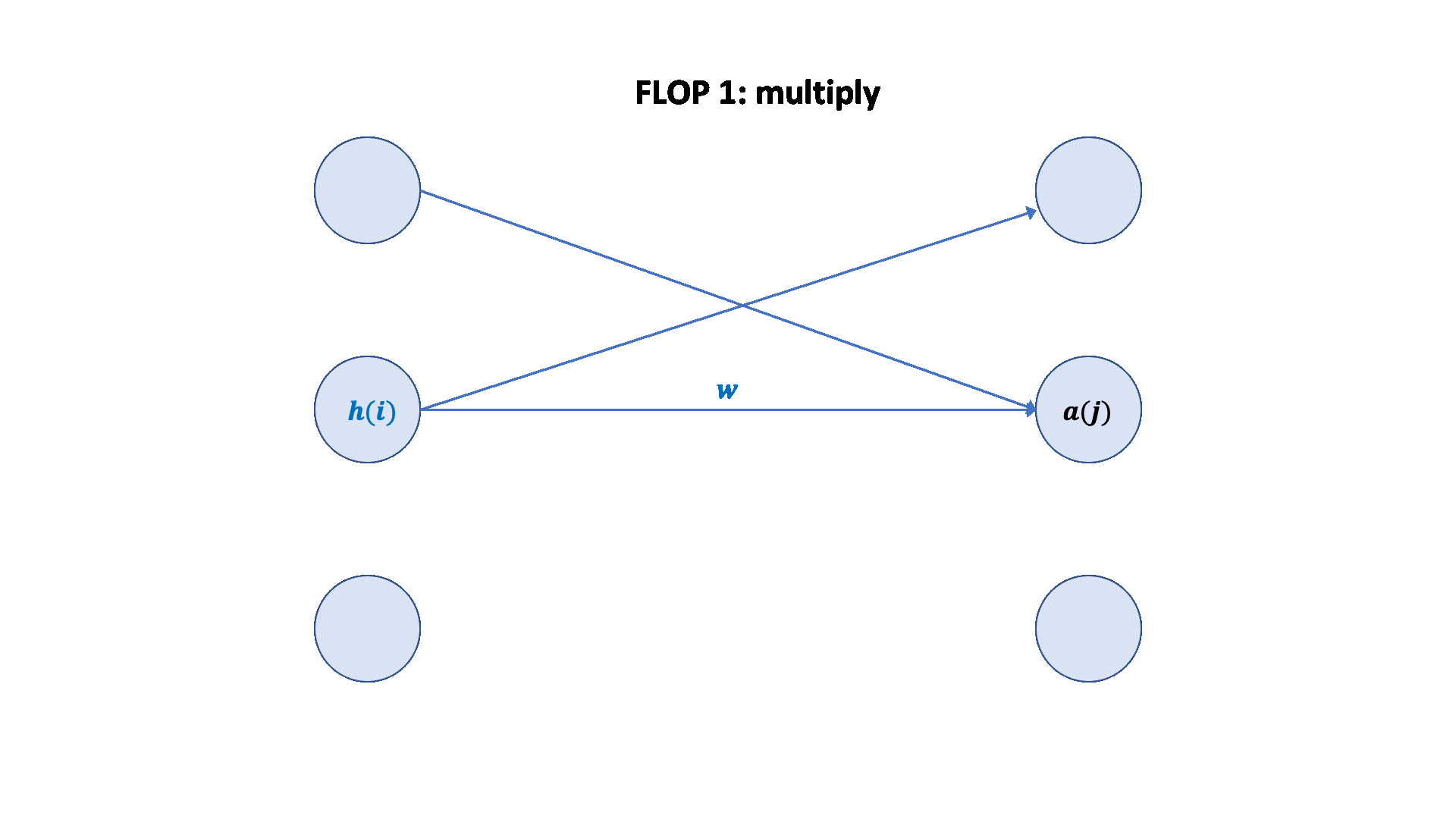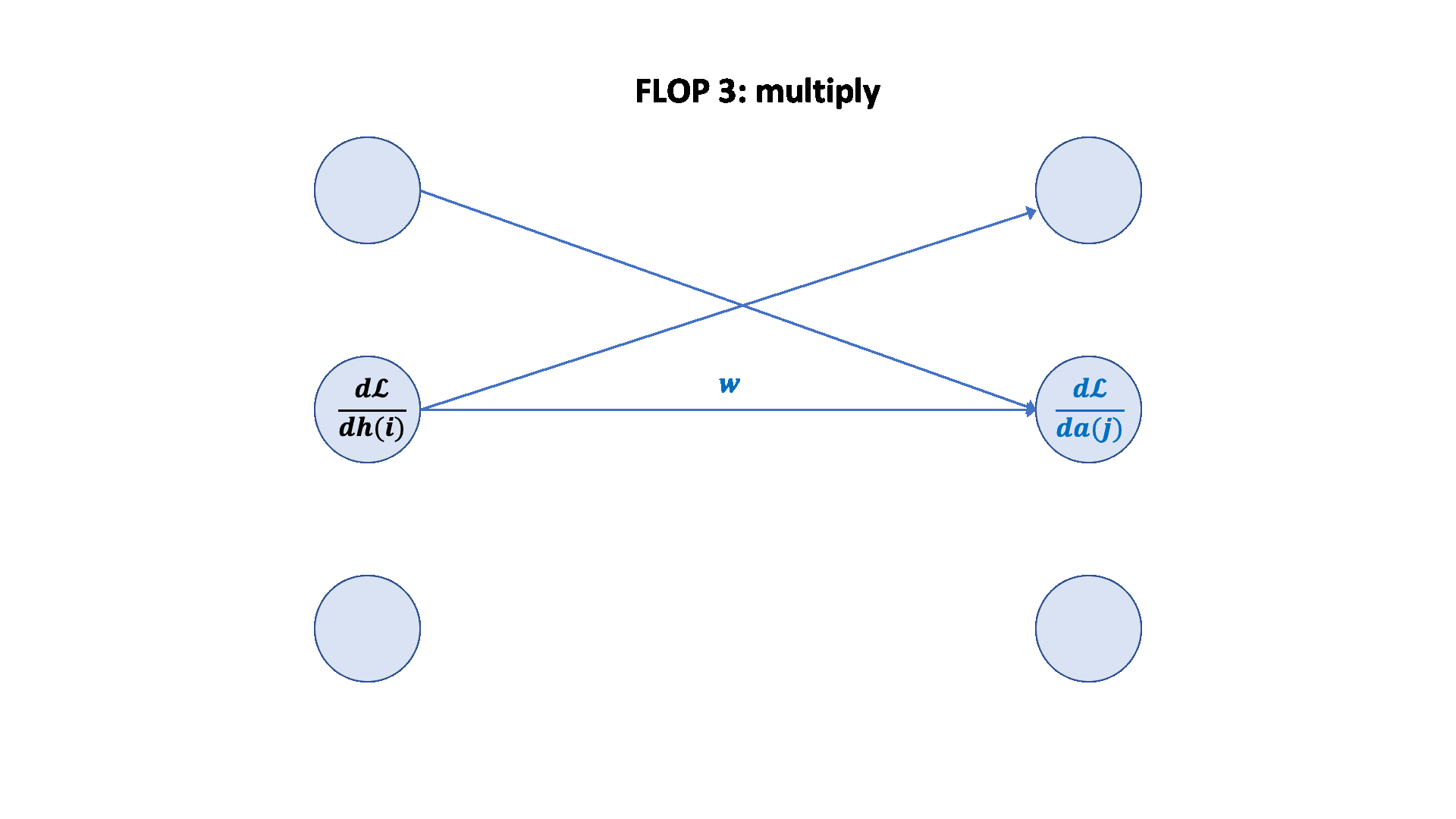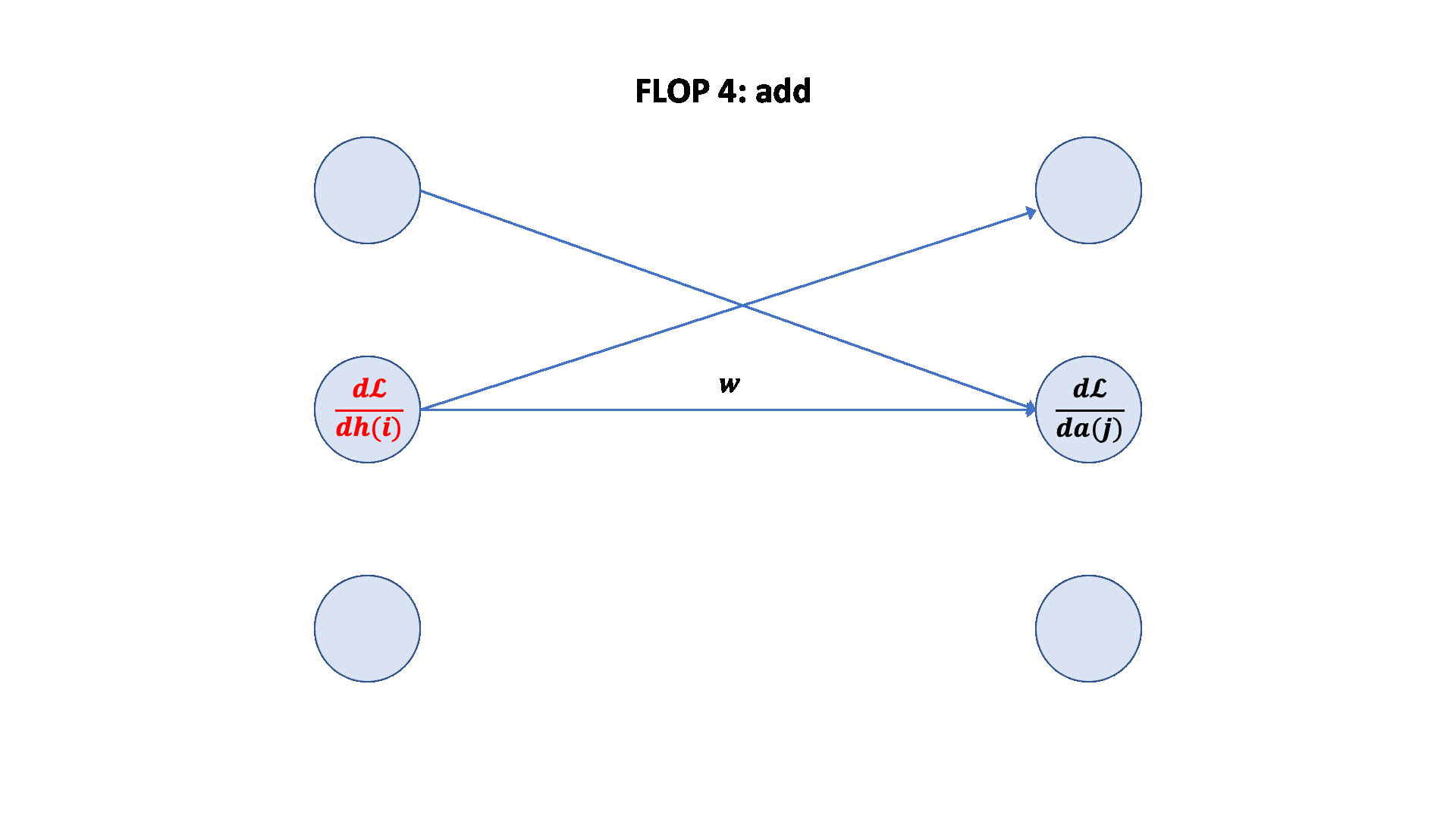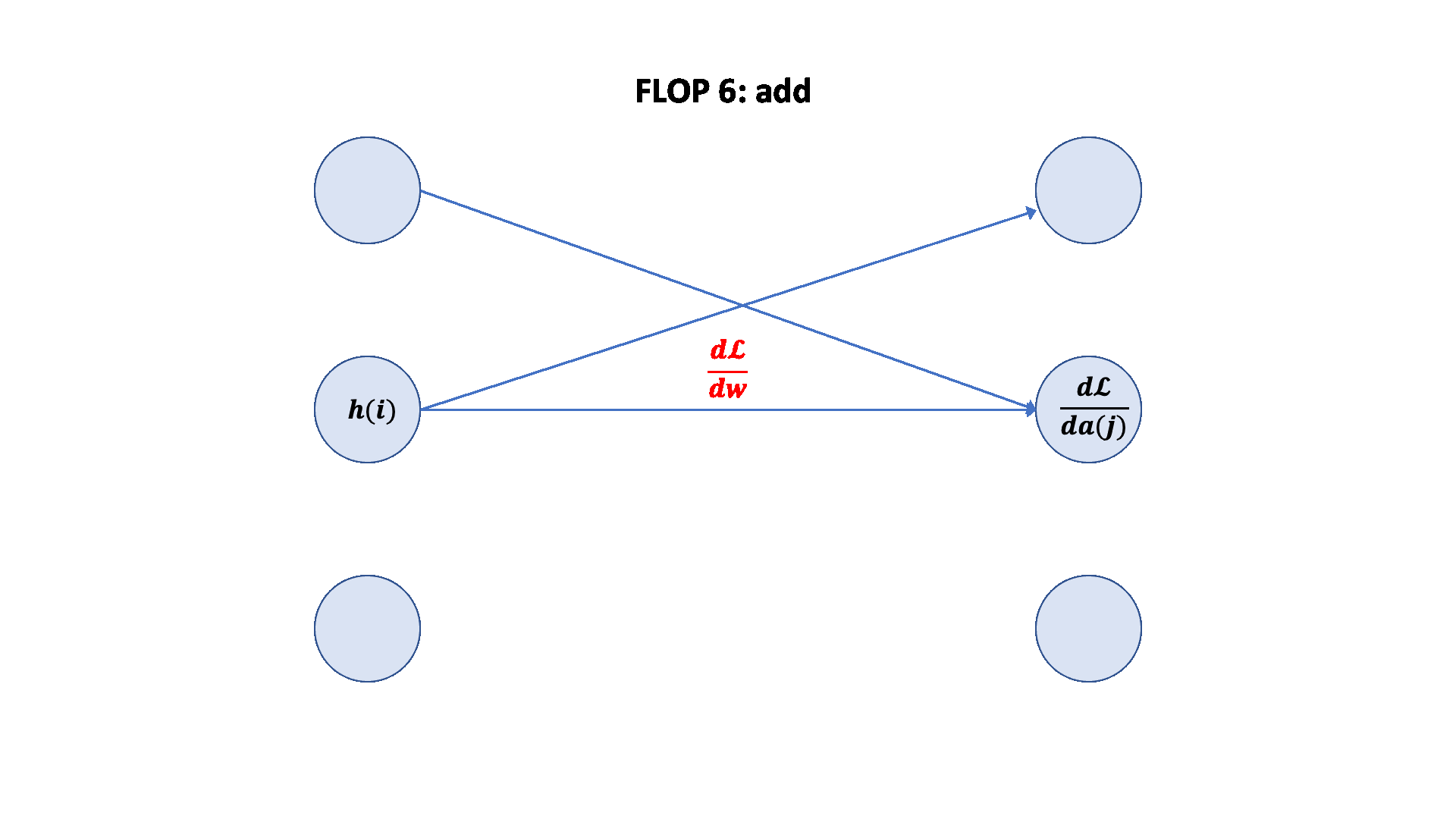
梯度 FLOPs 计算梯度(反向传播)的 FLOPs 通常是前向传播的几倍。
前向传播:2 * (# 数据点) * (# 参数) FLOPs
反向传播:4 * (# 数据点) * (# 参数) FLOPs
总计:6 * (# 数据点) * (# 参数) FLOPs
这个 6 * (# 数据点) * (# 参数) FLOPs 是一个常用的粗略估计,用于估算训练大型语言模型的计算量。
可视化:
模型 模块参数 模型参数存储为 nn.Parameter 对象,它们是特殊的张量,会被 PyTorch 自动跟踪梯度。
1 2 3 4 5 6 7 8 9 10 11 12 import torchfrom torch import nnimport numpy as npinput_dim = 16 output_dim = 32 w = nn.Parameter(torch.randn(input_dim, output_dim)) print (f"Type of w: {type (w)} " )print (f"Is w a Tensor? {isinstance (w, torch.Tensor)} " )print (f"Accessing underlying data: {type (w.data)} " )
参数初始化 参数初始化对训练的稳定性和收敛速度至关重要。不当的初始化可能导致梯度爆炸或消失。
1 2 3 4 5 6 7 x_input = torch.randn(input_dim) w_bad_init = nn.Parameter(torch.randn(input_dim, output_dim)) output_bad = x_input @ w_bad_init print (f"Output with bad initialization (first element): {output_bad[0 ]} " )
Xavier 初始化:通过 1/sqrt(input_dim) 重新缩放,使输出值与 input_dim 无关,有助于保持激活值的方差稳定。
1 2 3 4 5 w_xavier = nn.Parameter(torch.randn(input_dim, output_dim) / np.sqrt(input_dim)) output_xavier = x_input @ w_xavier print (f"Output with Xavier initialization (first element): {output_xavier[0 ]} " )
1 2 3 w_trunc_normal = nn.Parameter(nn.init.trunc_normal_(torch.empty(input_dim, output_dim), std=1 / np.sqrt(input_dim), a=-3 , b=3 )) print (f"Weight initialized with truncated normal:\n{w_trunc_normal} " )
自定义模型 使用 nn.Parameter 和 nn.Module 构建简单的深度线性模型。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 import torchfrom torch import nnimport numpy as npdef get_device (): return torch.device("cuda" if torch.cuda.is_available() else "cpu" ) class Linear (nn.Module): def __init__ (self, input_dim: int , output_dim: int ): super ().__init__() self.weight = nn.Parameter(torch.randn(input_dim, output_dim) / np.sqrt(input_dim)) def forward (self, x: torch.Tensor ) -> torch.Tensor: return x @ self.weight class Cruncher (nn.Module): def __init__ (self, dim: int , num_layers: int ): super ().__init__() self.layers = nn.ModuleList([ Linear(dim, dim) for i in range (num_layers) ]) self.final = Linear(dim, 1 ) def forward (self, x: torch.Tensor ) -> torch.Tensor: B, D = x.size() for layer in self.layers: x = layer(x) x = self.final(x) assert x.size() == torch.Size([B, 1 ]) x = x.squeeze(-1 ) assert x.size() == torch.Size([B]) return x D = 64 num_layers = 2 model = Cruncher(dim=D, num_layers=num_layers) param_sizes = [ (name, param.numel()) for name, param in model.state_dict().items() ] print (f"Model parameter sizes: {param_sizes} " )def get_num_parameters (model ): return sum (p.numel() for p in model.parameters()) num_parameters = get_num_parameters(model) print (f"Total number of parameters: {num_parameters} " )device = get_device() model = model.to(device) print (f"Model device: {next (model.parameters()).device} " )B = 8 x_data = torch.randn(B, D, device=device) y_output = model(x_data) print (f"Input data shape: {x_data.size()} " )print (f"Output data shape: {y_output.size()} " )
训练循环和最佳实践 随机性注意事项 随机性出现在参数初始化、Dropout、数据排序等许多地方。为确保可复现性,建议为每次随机性使用不同的随机种子。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 import torchimport numpy as npimport randomdef set_seed (seed ): torch.manual_seed(seed) np.random.seed(seed) random.seed(seed) print (f"Random seed set to {seed} " ) set_seed(0 ) print (f"Torch random number: {torch.randn(1 )} " )print (f"NumPy random number: {np.random.rand(1 )} " )print (f"Python random number: {random.random()} " )
数据加载 语言模型中的数据是整数序列(由分词器输出)。通常,数据量非常大,不能一次性加载到内存中。
将数据序列化为 NumPy 数组。
使用 np.memmap 惰性加载数据,避免一次性加载全部数据到内存(例如 LLaMA 数据为 2.8TB)。memmap 允许像访问内存数组一样访问磁盘上的文件。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 import numpy as npimport torchorig_data = np.array([i for i in range (1 , 101 )], dtype=np.int32) orig_data.tofile("data.npy" ) print (f"Original data saved to data.npy: {orig_data} " )data_memmap = np.memmap("data.npy" , dtype=np.int32, mode='r' ) print (f"Data loaded with memmap (first 10 elements): {data_memmap[:10 ]} " )print (f"Is data_memmap equal to original data? {np.array_equal(data_memmap, orig_data)} " )def get_batch (data: np.array, batch_size: int , sequence_length: int , device: str ) -> torch.Tensor: start_indices = torch.randint(len (data) - sequence_length, (batch_size,)) x = torch.tensor([data[start:start + sequence_length] for start in start_indices]) return x.to(device) B = 2 L = 4 x_batch = get_batch(data_memmap, batch_size=B, sequence_length=L, device=get_device()) print (f"Example batch from data loader (shape: {x_batch.size()} ):\n{x_batch} " )
固定内存 (Pinned Memory) 默认情况下,CPU 张量在分页内存中。通过 pin_memory() 将其固定在可分页内存中,可以允许从 CPU 异步复制到 GPU,从而提高数据传输效率。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 import torchif torch.cuda.is_available(): cpu_tensor = torch.randn(10 , 10 ) print (f"CPU tensor device: {cpu_tensor.device} " ) pinned_tensor = cpu_tensor.pin_memory() print (f"Pinned tensor device: {pinned_tensor.device} " ) gpu_tensor = pinned_tensor.to("cuda" , non_blocking=True ) print (f"GPU tensor device (non_blocking): {gpu_tensor.device} " ) else : print ("CUDA is not available. Pinned memory demonstration skipped." )
优化器 优化器负责根据计算出的梯度更新模型参数。本节介绍了几种常见的优化器。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 import torchimport torch.nn.functional as Ffrom torch import nnfrom typing import Iterabledef get_device (): return torch.device("cuda" if torch.cuda.is_available() else "cpu" ) class Linear (nn.Module): def __init__ (self, input_dim: int , output_dim: int ): super ().__init__() self.weight = nn.Parameter(torch.randn(input_dim, output_dim) / np.sqrt(input_dim)) def forward (self, x: torch.Tensor ) -> torch.Tensor: return x @ self.weight class Cruncher (nn.Module): def __init__ (self, dim: int , num_layers: int ): super ().__init__() self.layers = nn.ModuleList([ Linear(dim, dim) for i in range (num_layers) ]) self.final = Linear(dim, 1 ) def forward (self, x: torch.Tensor ) -> torch.Tensor: B, D = x.size() for layer in self.layers: x = layer(x) x = self.final(x) x = x.squeeze(-1 ) return x class SGD (torch.optim.Optimizer): def __init__ (self, params: Iterable[nn.Parameter], lr: float = 0.01 ): super (SGD, self).__init__(params, dict (lr=lr)) def step (self ): for group in self.param_groups: lr = group["lr" ] for p in group["params" ]: if p.grad is None : continue grad = p.grad.data p.data -= lr * grad class AdaGrad (torch.optim.Optimizer): def __init__ (self, params: Iterable[nn.Parameter], lr: float = 0.01 ): super (AdaGrad, self).__init__(params, dict (lr=lr)) def step (self ): for group in self.param_groups: lr = group["lr" ] for p in group["params" ]: if p.grad is None : continue state = self.state[p] grad = p.grad.data g2 = state.get("g2" , torch.zeros_like(grad)) g2 += torch.square(grad) state["g2" ] = g2 p.data -= lr * grad / torch.sqrt(g2 + 1e-5 ) B = 2 D = 4 num_layers = 2 model = Cruncher(dim=D, num_layers=num_layers).to(get_device()) optimizer = AdaGrad(model.parameters(), lr=0.01 ) x_opt = torch.randn(B, D, device=get_device()) y_target = torch.tensor([4. , 5. ], device=get_device()) pred_y = model(x_opt) loss = F.mse_loss(input =pred_y, target=y_target) print (f"Initial model parameters (first layer weight):\n{model.layers[0 ].weight.data} " )loss.backward() optimizer.step() print (f"Model parameters after one optimization step (first layer weight):\n{model.layers[0 ].weight.data} " )optimizer.zero_grad(set_to_none=True ) print ("Gradients cleared." )
内存 训练模型所需的总内存是参数、激活、梯度和优化器状态内存的总和。
参数内存:模型中所有参数的内存。
激活内存:前向传播过程中各层输出的激活值的内存。
梯度内存:与参数对应的梯度内存。
优化器状态内存:优化器(如 AdamW)可能需要额外的状态(如动量、方差估计)来更新参数。
假设 float32 (4 字节/元素):
总内存 = 4 * (参数数量 + 激活数量 + 梯度数量 + 优化器状态数量)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 D = 4 num_layers = 2 B = 2 num_parameters = (D * D * num_layers) + D print (f"Number of parameters: {num_parameters} " )num_activations = B * D * num_layers print (f"Number of activations (estimated): {num_activations} " )num_gradients = num_parameters print (f"Number of gradients: {num_gradients} " )num_optimizer_states = num_parameters print (f"Number of optimizer states (AdaGrad): {num_optimizer_states} " )total_memory_bytes = 4 * (num_parameters + num_activations + num_gradients + num_optimizer_states) print (f"Total estimated memory (bytes, float32): {total_memory_bytes} " )print (f"Total estimated memory (MB, float32): {total_memory_bytes / (1024 **2 ):.2 f} MB" )
计算 (一步) 对于一步训练(前向传播 + 反向传播),总 FLOPs 大致为:
FLOPs = 6 * B * num_parameters
1 2 3 flops_one_step = 6 * B * num_parameters print (f"Estimated FLOPs for one training step: {flops_one_step} " )
训练循环 一个典型的训练循环包括数据获取、前向传播、损失计算、反向传播、参数更新和梯度清零。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 import torchimport torch.nn.functional as Fdef get_device (): return torch.device("cuda" if torch.cuda.is_available() else "cpu" ) class Linear (nn.Module): def __init__ (self, input_dim: int , output_dim: int ): super ().__init__() self.weight = nn.Parameter(torch.randn(input_dim, output_dim) / np.sqrt(input_dim)) def forward (self, x: torch.Tensor ) -> torch.Tensor: return x @ self.weight class Cruncher (nn.Module): def __init__ (self, dim: int , num_layers: int ): super ().__init__() self.layers = nn.ModuleList([ Linear(dim, dim) for i in range (num_layers) ]) self.final = Linear(dim, 1 ) def forward (self, x: torch.Tensor ) -> torch.Tensor: B, D = x.size() for layer in self.layers: x = layer(x) x = self.final(x) x = x.squeeze(-1 ) return x class SGD (torch.optim.Optimizer): def __init__ (self, params: Iterable[nn.Parameter], lr: float = 0.01 ): super (SGD, self).__init__(params, dict (lr=lr)) def step (self ): for group in self.param_groups: lr = group["lr" ] for p in group["params" ]: if p.grad is None : continue grad = p.grad.data p.data -= lr * grad def get_batch_train (B: int , D: int , true_w: torch.Tensor ) -> tuple [torch.Tensor, torch.Tensor]: x = torch.randn(B, D).to(get_device()) true_y = x @ true_w return (x, true_y) def train ( name: str , get_batch_fn, D: int , num_layers: int , B: int , num_train_steps: int , lr: float print (f"\n--- Starting training for: {name} ---" ) model = Cruncher(dim=D, num_layers=num_layers).to(get_device()) optimizer = SGD(model.parameters(), lr=lr) true_w = torch.arange(D, dtype=torch.float32, device=get_device()) for t in range (num_train_steps): x, y = get_batch_fn(B=B, D=D, true_w=true_w) pred_y = model(x) loss = F.mse_loss(pred_y, y) loss.backward() optimizer.step() optimizer.zero_grad(set_to_none=True ) if (t + 1 ) % (num_train_steps // 5 ) == 0 or t == 0 : print (f"Step {t+1 } /{num_train_steps} , Loss: {loss.item():.4 f} " ) print (f"--- Training for {name} finished ---" ) train("simple_run" , get_batch_train, D=16 , num_layers=0 , B=4 , num_train_steps=10 , lr=0.01 ) train("hyperparameter_tuning_lr_0.1" , get_batch_train, D=16 , num_layers=0 , B=4 , num_train_steps=10 , lr=0.1 )
检查点 训练大型语言模型需要很长时间,并且可能会因为各种原因中断。为了避免丢失所有进度,建议定期将模型和优化器状态保存到磁盘(创建检查点)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 import torchdef get_device (): return torch.device("cuda" if torch.cuda.is_available() else "cpu" ) class Linear (nn.Module): def __init__ (self, input_dim: int , output_dim: int ): super ().__init__() self.weight = nn.Parameter(torch.randn(input_dim, output_dim) / np.sqrt(input_dim)) def forward (self, x: torch.Tensor ) -> torch.Tensor: return x @ self.weight class Cruncher (nn.Module): def __init__ (self, dim: int , num_layers: int ): super ().__init__() self.layers = nn.ModuleList([ Linear(dim, dim) for i in range (num_layers) ]) self.final = Linear(dim, 1 ) def forward (self, x: torch.Tensor ) -> torch.Tensor: B, D = x.size() for layer in self.layers: x = layer(x) x = self.final(x) x = x.squeeze(-1 ) return x class AdaGrad (torch.optim.Optimizer): def __init__ (self, params: Iterable[nn.Parameter], lr: float = 0.01 ): super (AdaGrad, self).__init__(params, dict (lr=lr)) def step (self ): for group in self.param_groups: lr = group["lr" ] for p in group["params" ]: if p.grad is None : continue state = self.state[p] grad = p.grad.data g2 = state.get("g2" , torch.zeros_like(grad)) g2 += torch.square(grad) state["g2" ] = g2 p.data -= lr * grad / torch.sqrt(g2 + 1e-5 ) model = Cruncher(dim=64 , num_layers=3 ).to(get_device()) optimizer = AdaGrad(model.parameters(), lr=0.01 ) checkpoint = { "model_state_dict" : model.state_dict(), "optimizer_state_dict" : optimizer.state_dict(), "epoch" : 10 , "loss" : 0.05 } torch.save(checkpoint, "model_checkpoint.pt" ) print ("Checkpoint saved to model_checkpoint.pt" )loaded_checkpoint = torch.load("model_checkpoint.pt" ) loaded_model = Cruncher(dim=64 , num_layers=3 ).to(get_device()) loaded_optimizer = AdaGrad(loaded_model.parameters(), lr=0.01 ) loaded_model.load_state_dict(loaded_checkpoint["model_state_dict" ]) loaded_optimizer.load_state_dict(loaded_checkpoint["optimizer_state_dict" ]) print ("Checkpoint loaded successfully." )print (f"Loaded epoch: {loaded_checkpoint['epoch' ]} " )print (f"Loaded loss: {loaded_checkpoint['loss' ]} " )
混合精度训练 数据类型(float32、bfloat16、fp8)各有优缺点。为了兼顾精度、内存和计算效率,可以采用混合精度训练。
高精度 : 更准确/稳定,更多内存,更多计算。低精度 : 精度/稳定性较低,更少内存,更少计算。
如何兼顾?
解决方案:默认使用 float32,但在可能的情况下使用 bfloat16 或 fp8。
通过混合精度训练,可以在保持模型性能的同时,显著减少内存占用和提高训练速度。