数字信号处理FFT快速傅立叶变换MATLAB实现——实例
今天做作业的时候发现要对一个信号进行FFT变换,在网上找了半天也没找到个能看懂的(因为我太菜了),后来自己研究了一下,感觉一知半解的
起因是这道作业题
例题-满足奈奎斯特

我画了两个图,一个是原信号经过采样后的离散图,一个就是此信号经过FFT后的频谱图
因为是8kHZ采样,所以信号不会失真,频谱也是正确的
解答如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| clear
close all
clc
fs=8000;%采样频率
n=0:99;%采样点100个
y=sin(0.00625*2*pi*n)+sin(0.0625*pi*2*n)+sin(0.125*2*pi*n);%采样后的信号 0.00625=50/8000
subplot(2,1,1);
stem(n,y)
title('抽样后信号的时域图像')
xlabel('n');ylabel('幅值');
Y = fft(y);%进行fft变换
f=(0:length(Y)-1)*fs/length(Y);%在频域,转换坐标为f,f= n*(fs/N)=Y的长度*采样频率,还是8k,但是在Matlab需要经过这样的运算
subplot(2,1,2)
stem(f,abs(Y));
title('信号频谱图')
xlabel('f/Hz')
ylabel('幅度')
|
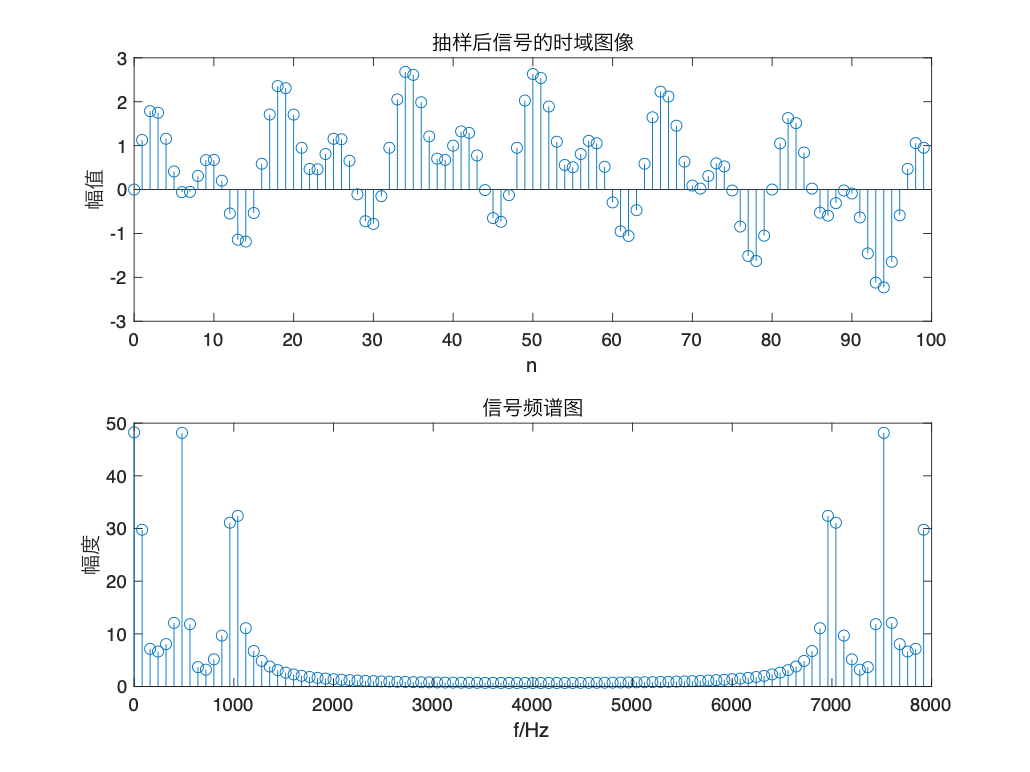
那么,如果采样频率没有满足奈奎斯特抽样定律,会发生什么呢
正好作业的第二道题就是不满足的
例题-不满足奈奎斯特

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| clear
close all
clc
fs=800;%采样频率
n=0:99;%采样点100个
y=sin(0.0625*2*pi*n)+sin(0.625*pi*2*n)+sin(1.25*2*pi*n);%采样后的信号 0.00625=50/8000
subplot(2,1,1);
stem(n,y)
title('抽样后信号的时域图像')
xlabel('n');ylabel('幅值');
Y = fft(y);%进行fft变换
f=(0:length(Y)-1)*fs/length(Y);%在频域,转换坐标为f,f= n*(fs/N)=Y的长度*采样频率,还是8k,但是在Matlab需要经过这样的运算
subplot(2,1,2)
stem(f,abs(Y));
title('信号频谱图')
xlabel('f/Hz')
ylabel('幅度')
|
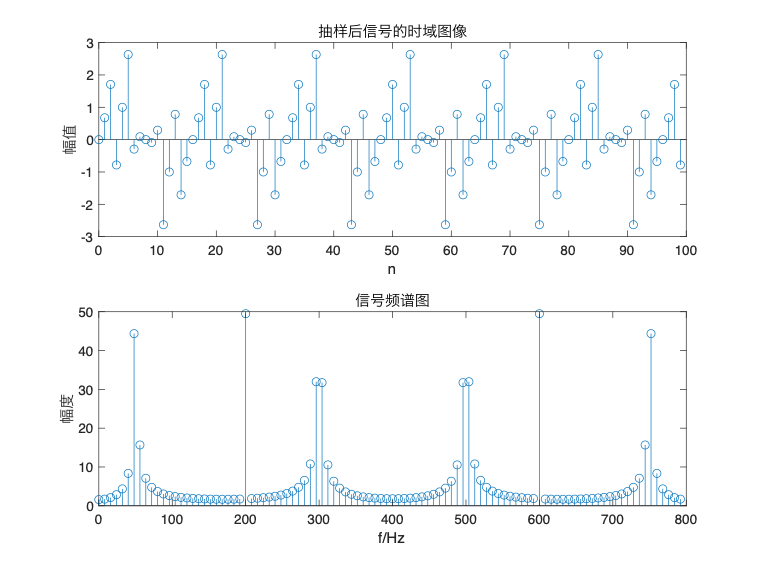
感觉和想象中不太一样,我还以为会乱成一片,那么经过观察,我们可以看到,在200HZ和300HZ出现了峰值,为啥在这里呢
因为以400HZ为对称轴的话,500HZ就走到400HZ那里又原路返回,1000HZ也同理
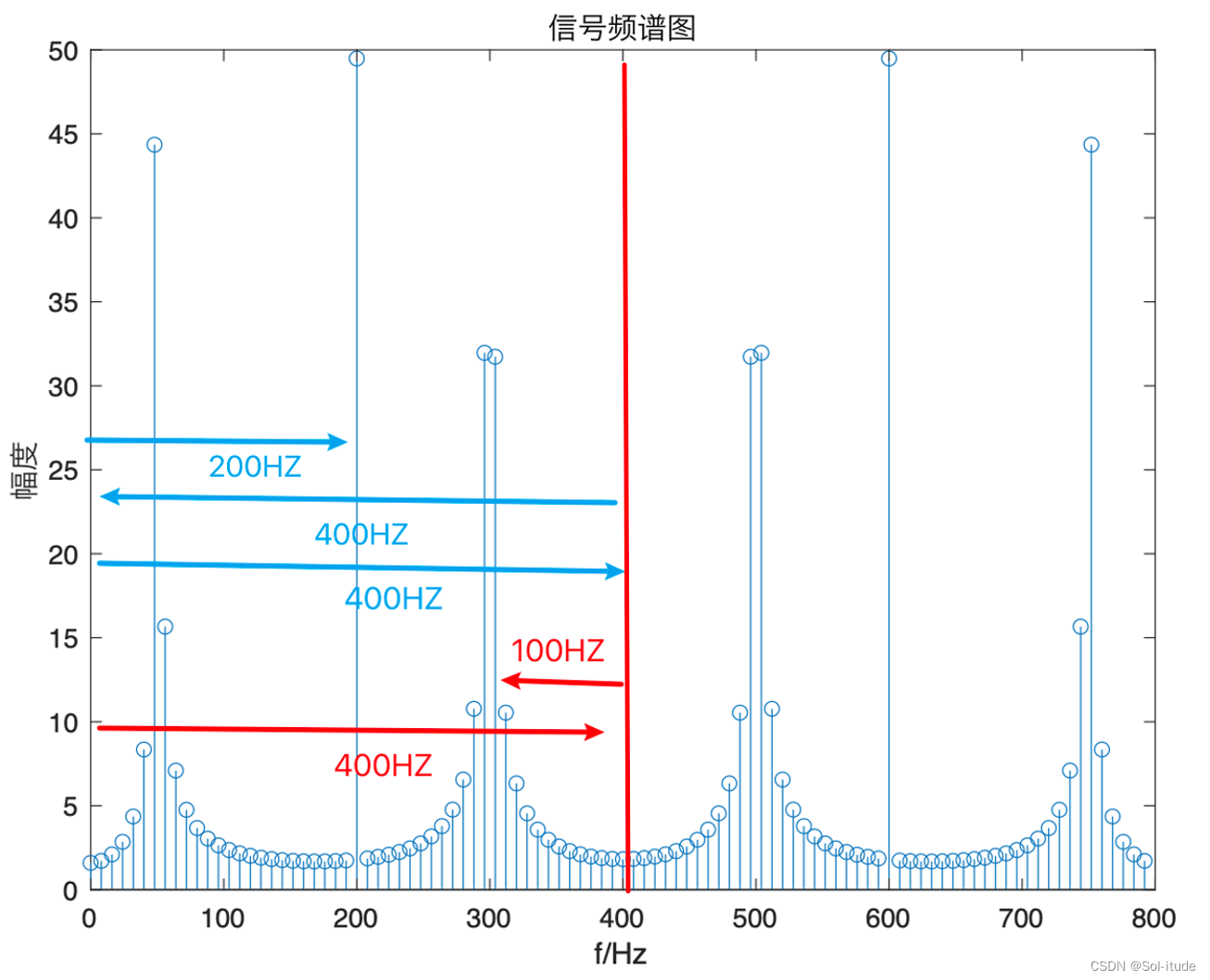
500HZ变成了红色的400HZ+100HZ
1000HZ变成了蓝色的400HZ+400HZ+200HZ
这就是频谱失真的情况
后续思考
然后看了这个,在上课时我又问了老师一个很弱智的问题
既然频谱不是混乱的,那倒着推出未失真的信号不就行了?
后来得到解答,仔细想一想就能发现,假如在200HZ幅度很大,那他既有可能是200HZ,也有可能是600HZ,也有可能是1000HZ等等,其实就是无限的
所以说即使是向上图那样的情况,也依旧不可能知道原信号的频率









